Apply matrix to neural network computation

Now that you understand the basics, let’s see how we can apply matrix to neural network computation.

Let’s using the variables in our neural networks.

Before, the calculation formula we use is as follows:

$a_1 = w_{1,1}x_1+w_{2,1}x_2 + b_1$ $a_2 = w_{1,2}x_1+w_{2,2}x_2 + b_2$ $a_3 = w_{1,3}x_1+w_{2,3}x_2 + b_3$

Now, we use matrix to represent:

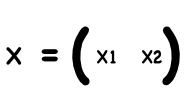
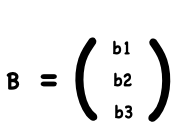
W is the matrix of weights, X is the matrix of inputs, B is the bias.

The formula for calculating the input of the hidden layer is as follows

$A = XW + B$

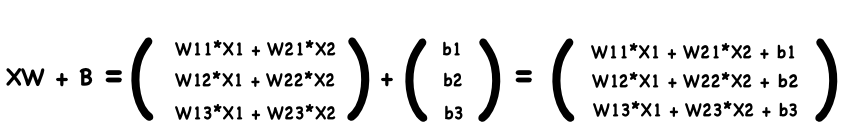
xw+b.png

We use a simple matrix operation expression $A = XW + B$ to calculate the input of the hidden layer node. Even if we add more nodes, the formula will be the same. It’s pretty neat and powerful.

Let’s use Numpy for hidden layer node calculations.

import numpy as np
X = np.array([x1, x2])
W = np.array([[w11, w12, w13], [w21, w22, w23]])
B = np.array([b1, b2, b3])

A = np.dot(X,W) + B
print(A)

[1.    1.34  1.188]

Z = sigmoid(A)
print(Z)

[0.73105858 0.79248994 0.76638318]

The calculation process looks a lot cleaner than it did before.